Below you’ll find the link to a draft of my thesis. I’d be happy to have comments, specifically on the 2nd part about the Epsilon Network. You don’t really need a sciency background to have a look, and comments can be about anything from errors in the figures to general ideas or grammar errors.
Open your favorite PDF reader and use the comment function, or just comment below or on twitter with the page number.
If you give me your name I’ll put you in the acknowledgements. Thanks for your help!
We all know the basics behind Darwinian evolution. Individuals from a species are born with different traits and the fittest members have more offspring, which share some of these “winning traits”. Antelopes become faster, giraffes become taller, etc.
Nevertheless, selection pressures do not always affect a species as a uniform group. In fact, the most interesting examples of competition arguably occur between different groups in the same species. This tells a more complicated story than the monolithic interspecies competition (e.g. prey vs predator), or even than individual fitness against the rest of the species (tall giraffe vs all other giraffes, male vs other males). That is why I call it Intraspecific Group Arm Race.
Today I would like to talk about how these strange pressures appear and what they entail. As usual, this post is not a summary of a current consensus, but a personal reflexion.
The most famous example of intraspecific group competition must be the evolutionary arm race between males and females mallards. Sexual arm races exist in dolphins, flies, beetles and many other species, but ducks are the most popular example for online news (and I just know the following paragraph should increase traffic to my blog tenfold…).
Mallards have complicated sex lives. You see, single males like raping females, and females do not like being raped by males. Therefore they both evolved complicated genitals: males have long, corkscrew shaped penises; females have even more gigantic, corkscrew shaped vaginas. (Maybe I should write this once more to be sure to attract the internet crowds?)
The race for complex genitals occurs because single males have an interest in fathering at least some ducklings rather than zero, while females have an interest in choosing the best father for their offspring (and not just the most rapey one). Thanks to their convoluted vagina, females can control who fertilizes the eggs: their active cooperation is required for the male to succeed. The sexes both continuously evolve to trump each other’s adaptations. Most birds don’t even have penises, so the evolutionary pressure must definitely be strong.
Arm races occur whenever you have competition. But for intraspecific group arm race to start, you need to satisfy these four requirements:
A group is defined as an ensemble of individuals who are on the same side of the competition for a resource at some point in time: male/female/asexued, cheater/cheated, adults/kids. In the ducks case, 1. the 2 groups are single males vs females. 2. They are all mallards (rule 2 is a corollary of rule 4, but let us still write it explicitly). 3. They compete for a choice: who gets to choose the genetic makeup of the ducklings? The cost of losing for the unpaired male is not passing his genes on. If he can father even 1 duckling, that is the difference between the life or death of his entire lineage! The female on the other hand, always passes her genome on: for her the cost is spending energy to raise ducklings that have unwanted genes and might not all survive and reproduce. 4. The ducklings can be born male or female: they can end up on any side of the competition. This last condition prevents one side from “winning”: an ideal genome would give you strong male offspring AND strong female offspring, otherwise you’re sentencing half of your own descendants to losing the game.
Groups do not have to be as classical as male vs female.
Take human babies vs human parents. Have you noticed that babies cry a lot (Yes, you have…)? Let’s be honest, a lot of the time it seems that they cry for no specific reason and nothing but time will calm them down.
One theory, not uncontroversial but backed up by interesting data, is that babies cry day and night both to exhaust their parents and to extend the post-birth infertility of their mother (linked to breastfeeding). The end goal being that no other sibling should be born too early so the baby can have the parents’ full attention and grow with all the physical and emotional resources available (like milk, cuddles and peekaboo parties). Human babies and human adults compete for the adult’s energy: the conflict arises from the fact that the baby fares better if the parents don’t make another baby too soon, but the parents fitness would be increased by 1. Not being exhausted and 2. Having as many babies as possible. Babies should evolve to be as noisy and stressful as possible, while parents evolve to discriminate unmotivated crying and ignore it. But the arm race is contained within the species: the baby is supposed to in turn join to the “parents” group. An ultra effective crying baby would turn into a very miserable parent. Again, the tug-o-war is balanced.
This brings us to the critical idea of unbalanced costs. Two competing groups have to mitigate the costs for their opponents cum future offspring, but what about the costs at the scale of the species? There is no baked-in rule preventing an arm race from being costly to the species. Some scientists say that a successful mutation must increase the fitness of the whole species, otherwise the mutation would be weeded out. I think that something much more interesting happens.
Can a mutation be beneficial for an individual and damaging for its species? Yes. Some very aggressive male ducks end up drowning unlucky females. From their point of view, there is no loss: if the female resists so much that she dies, the male probably wouldn’t have managed to fertilize the egg anyway. Remember, for those single males, just one duckling is the difference between life and death of their entire lineage. It is highly beneficial for them to be overly aggressive, and to spread their aggressive genes. At the scale of the species though, the cost is high. These female ducks could have raised many generations of ducklings. But no individual acts with an entire species in mind: even on the brink of extinction, the aggressive males would likely not be able to “just stop drowning uncooperative females”, as females would not be able to “just stop being uncooperative and accept unwanted genes”. There is no magical stop switch, “think about the species before yourself” button: arms races can go wrong.
And yet. Restraints can evolve and enhance stability. I will always remember Justin Werfel’s talk about evolved death. A major dominant theory is that death has no evolutionary advantage, and therefore no species will ever evolve to have its members die younger rather than older. After all, if you die, you loose on occasions of passing your genes on.
But during the last 15 years, evidence for the evolution of death has accumulated. More generally, in a space where resources are limited, a population that has self restraint mechanisms will survive better than a population of reckless individuals. Imagine a group of cows devouring all of the grass at once, not allowing it to grow back. They face immediate reward as they fatten but long term starvation as the grass just dies from exhaustion. Now imagine if one of the cows has a mutation for restraint. Maybe it’s a dwarf cow, or maybe it dies after only a few years. Anyway, the grass were this cow and its descendants live will be healthier than elsewhere, and on the long term they will, as a group, survive where the others starve and die.
Restraints are counter intuitive in a classical evolutionist view, because evolution is not supposed to look into the future. If I can have more kids than you right now, I am fitter than you and will supplant you. But this view fails to take into consideration environmental feedback, which can be quite immediate. The fasting cows only survive because they share the same physical space, allow their own offspring to inherit it and protect their turf from outsiders. If the voracious cows could just come up and eat what the fasting cows have saved up, this would not work. The environment must be inherited and protected just as the genes are.
So there is no need for evolution to “look into the future” to favor less costly arm races, and there is no guarantee that the arm race offers any advantage to the species either.
This becomes particularly interesting when you start considering other, more abstract groups satisfying the conditions for intraspecific group arm race. Take cheaters and vigilantes. The transmission does not even have to be genetic. When you find out a new way to cheat, you have an immediate advantage. But you also become able to spot people who cheat in the same way as you. So if you teach your offspring or other in-groups how to cheat, they also have an advantage but they cannot use it against you or their siblings. The more successful your cheating strategy is, the more offspring you transmit it to, and… the less successful it becomes. The greater honeyguide is a good example of cheating dynamics. These birds lay an egg in other birds’ nests. But they have also evolved to notice if another honeyguide has already left an egg there, and destroy that egg. So they have to evolve eggs that look more and more like the parasited bird species, to avoid being crushed by their fellow cheaters; but they also have to become better and better at spotting suspicious eggs… Here the two groups are simply the 1st honeyguide to lay an egg vs the ones that come after. Whether a bird will belong to one or the other group is pretty much random. All conditions are respected for a perfect intraspecific group arm race. Yet there is a big loser in the story: the parasited bird. None of its own offspring survives, only the honeyguide chick. And if the competition between honeyguides is so harsh already, it must mean that almost all nests get parasited, several times in a row! The bird could well get parasited to extinction.
Unless, that is, a mutation for restraint appears first and the conditions for its protection are satisfied…
We have seen that these interesting competitive dynamics can happen for concrete, classical groups defined by their genes, only redistributed once per generation; to groups defined by their age, with a total permutation halfway through the generation; to the more abstract who-came-first groups that change every time a honeyguide visits a nest. This framework seems highly robust and its preconditions are so loose that it seems likely to have a large, underestimated influence on the evolution of species.
What about leaders vs followers? 1st child vs following siblings?
How many other groups can you find out?
Yesterday I read this piece by Shaun King. I know a few countries that, viewed from the outside, look obsessed by the idea that they are “the best place in the world”. Even without going that far, many countries like to brag (to outsiders too, but mostly to themselves) that they have the best [insert your answer here] in the world. French people have a reputation for being pretentious, but also for complaining a lot about their homeland. Today I will indulge in the latter. We all know what feels good about our countries, but do we know about what’s really bad about them?
“The 1st step to solving a problem is to recognise that there is a problem.” In this post, I will just go through the same topics as King did and discuss the ranking of France through some indicators. What are we good at, and what should we be really focusing on improving right now?
Disclaimer 1: Some people’s go-to answer to any nation-based criticism is “Leave if you don’t like it here.” A. Criticising does not mean you hate a place, and B. I already left, I don’t live in France anymore. As far as I can tell, that did not make our county’s issues suddenly disappear…
Disclaimer 2: Yes, yes, I am addressing my fellow countrypeople, I should write in French. But I found that international opinions seem to count more for a certain breed of people than criticism from the inside…
Prisons and police
France ranks 147th out of 222 countries for prison population rate.The website prisonstudies has handy tools to navigate prison data. It’s not a terrible score, but it’s nothing to be proud of either. We have been putting more and more people in prison since 1992; in 2011 we had 102 people in prison per 100 000 inhabitants. More than 1 in 5 of these prisoners are not even convicted people; they are just waiting for a trial. But where we have a terrible record is on how we overstuff our prisons, putting people in really bad conditions – our prisons are running at 116.6% capacity, and the state has been repeatedly condemned for mistreatment, and even for not respecting basic human rights by the European Court of Human Rights. Not really what you would expect when you think “France”. Then there is the issue of police violence. It’s nothing comparable to what has been happening in the US, but who would take that as a standard? Tensions between the police and poorer suburbs are no state secret, sometimes culminating in assault in death. The thing is… we have official numbers on violence against police, but none about the violences committed by police. We do have emblematic cases of people, overwhelmingly POC, assaulted or killed by the police. Tensions between the police and the people are never a good sign; no numbers about police violence is not a good sign; and what’s really a bad sign is that we have been criticised by Amnesty International (fr) for the impunity of our policemen when they do commit violent acts on people. About 20 people are killed by the police every year, but there are rarely any consequences for the policemen, and that is what is criticised by Amnesty.
France’s prisons and police: Not outrageous, but lots to improve.
Health care
99.9% of the French have health insurance. In its study of health systems around the world, the World Health Organisation says: “France provides the best overall health care followed among major countries by Italy, Spain, Oman, Austria and Japan”. Wow! That’s something to be happy about. Being sick in France won’t make you bankrupt, although I do find the dentist expensive. French people have been worried for years about the future of their healthcare: “le trou de la secu”, the hole in the health system budget. But things are looking good as this deficit is planned to reach its lowest level in 2017. Issues with health care can rather be found in the working conditions of doctors (in 2005 France was found not to respect the limits on working time fixed by Europe), in the slowly dwindling numbers of doctors (fr), and in issues linked to gender: no official study here, but recent scandals have shown that women face gender-specific discrimination by medical professionals (this is unfortunately hardly a French specificity).
French Health Care: I’ve had a number of astonishingly bad experiences, but who am I to argue with the WHO? “Best overall health care”! Congrats, France.
Education
The PISA survey data can be found here. Compared to other countries in the OECD, we’re doing average in Science, and good in reading and gender equity. We’re doing really bad in equity between social backgrounds though, so bad in fact that we were ranked last in 2015. This report by the National Agency that evaluates French school system actually says that school is one of the causes of social inequalities. Don’t be born poor, and if you do, silly you, don’t go to a French school.
French Education System: average, but rife with inequalities.
Income inequality
In 2008, France was one of 5 OECD countries where income inequality was steadily decreasing (pdf). In 2013, we were ranked on a par with Germany and Hungary, still better than average but worse than in 2008. On the other hand, the gender wage gap of 14% had not budged since the 2000s, while it was decreasing from 18 to 15% in the whole OECD. At that rate we will soon be worse than the average, all because we haven’t evolved in 17 years.
French income inequality: Slightly better than average, but overall getting worse.
Quality of life
It’s no secret that French people used to pop up more antidepressant than anyone else in the world, but that’s not the case anymore. Let’s have a look at the Happiness Report: France ranks 31st out of 155 countries. Not bad at all! For a nation self-described as a country of whiners. The report explains French happiness in equal parts by the fact that they live in a rich country and by the strength of their social networks. We also have good life expectancy. However, we are apparently growing less and less happy, with one of the worse progression of the report, 24 places away from Venezuela (the worst progression). We’re still one of the most attractive countries for tourists although we are not the most competitive place for travel (pdf), we’re 2nd behind Spain. To be fair, Spain is where French people go when they need a break! It is worth noting that in terms of traveler safety (see also previous link), we are not even in the top 20. I don’t think a single tourist will be surprised by this news – it’s the most common complaint I hear.
French life: We’re getting less happy, but hey, at least we’re popping less pills. And it’s not that bad overall, especially if you are a traveler (but hold on your wallet).
Others
There topics were not in King’s piece, which makes sense because his was tailored for the US. France ranks as one of the worst European countries for English language proficiency, doing only slightly better than Japan on the world ranking. We rank best at preventing “preventable deaths” thanks to timely and effective care. We’re 39th on the free press ranking, good but still our worse position since 2013.
I just remembered that I have videos that I took of my OEE simulations. They go along with the OEE posts that you can find here: https://itakoyak.wordpress.com/?s=OEE
They’re not excellent quality and somehow I never thought about including the videos in the data post.
Wikimedia Commons
Close your eyes. I give you 2 planets to hold, one in each hand. One harbors life as we know it, the other is without life. Which one would you say feels hotter in your palm? Why?
Detecting life on faraway planets is a gigantic an fascinating issue. We can’t just go there and look; we can’t even have a proper look from Earth. We have to rely on noisy measures that come from instruments very different from the sensors we’re used to in our own bodies.
An even more thorny issue is that we are not really sure how to define life.
I once heard someone say that a characteristic of life it that it goes against the 2nd law of thermodynamics (exploration of the relationship between life and entropy actually goes back to Erwin Schrodinger). My first reaction was disbelief, which is ironic considering that my first reaction to hearing the 2nd law in high school was also disbelief.
You might have heard it presented like this: if you break an egg and mix it up, you will never be able to get it back to its original state (separated white and yolk) even if you mix it forever. Why? Because of the 2nd law, which says that the universe must always go towards more disorder (actual formulation: The total entropy of an isolated system must always increase over time or remain constant.)
I strongly disliked the example of the egg, with its fuzzy notion of “disorder”. I felt like the initial state was only special because my physics professor had decided so. What if I define another state as being special? I could record the position of each molecule after having mixed the egg for 20 seconds, and say that this is a very special state, and that any amount of mixing would not bring me back to that exact state. Therefore this sate must represent “order”. Then bringing the egg from its separated-white-and-yolk state to my special ordered state would be a decrease in entropy. The 2nd law did not make sense.
The notion of a relationship between an “order” and time made more sense in chemistry lessons, where everything “wants” to go to a state of lower energy. Electrons go to the lower orbits of the atom if they can find a free space. Spontaneous chemical reactions release energy, and non spontaneous ones require energy. And in mechanics, where everything also goes to the states of lower energy if given a chance. Balls go down hills, etc. But equating low energy with order in this way was just as wrong as my understanding of the egg example.
Entropy is a measure of statistical disorder. It is not applied to one state; it is the number of different microscopic states that a system could theoretically be in given a set of parameters. If you take cup of water, there is a given (enormous) number of positions at which each molecule can be: each one can be literally anywhere in the volume of the cup. If you now freeze the cup, each molecule has a reduced number of positions it could be in, because a crystal of ice has a specific structure and the molecules have to arrange themselves following that structure.
And here comes the relationship between entropy and beating an egg. The cup of ice has lower entropy than the cup of water. The non-beaten egg (each yolk particle must be in contact only with other yolk particles, except a fine layer; same for the white particles) has lower entropy than the beaten egg (each particle can be anywhere).
So what does it have to do with life? Consider the example of the egg. If it is such an organised structure, and the universe goes towards disorder, how could the atoms ever come together from a disorganised state and make such a highly organised, low entropy system as an egg? Order arising from disorder seems to defy the 2nd law. Entropy is sometimes defined as a measure of energy dispersal; does it mean that a planet with organised life everywhere would be colder than a planet without life?
It is mostly accepted that phenomenons seemingly going against the 2nd law do respect it when considered as part of a bigger system (there are several such cases besides life itself). You can make ordered ice from disordered water by channelling this disorder into the environment: it is the heat absorbed by your freezer. On average, the ice-freezer system still has the same entropy. So the egg must also come into existence at the expense of creating disorder somewhere else, and the 2nd law is respected. Maybe the 2 planets in our introduction would have the same average temperature.
These observations about the 2nd law and life do give us an interesting starting point to think about life definition and detection. You could say, like Lovelock when asked how to detect life on Mars, that entropy reduction is a characteristic of life.
But I would like to talk in terms of temporal patterns in energy. I haven’t really seen this discussed elsewhere, but I confess not having looked a lot either.
Life requires some chemical reactions to take place. Chemical reactions tend to have preferred directions: those that release energy and therefore lead to lower states of energy. If you want to obtain other reactions, you have to deliver energy to the system. In addition, if you want some reactions to happen at a predefined timing or in a specific order, you have to control when the energy is delivered to the system.
So, if you want to broaden the set of chemical reactions available to you, you need a way to store energy (and some other things to get proper metabolism: a way to get energy for storage, and a way to schedule the desired reactions).
If you store energy, it means that you are taking energy from your environment; it also means that you prevent this energy from being released.
Finally, because no energy transfer can be perfect, by causing chemical reactions to happen you must also be releasing heat in the environment.
So one way to detect life could be to look for pockets of stored energy and heat that are isolated from the environment.
Back to our introduction, which planet would be hotter and why?
Consider what makes the basis of life on Earth: plants. Plants feed on sunlight, animals feed on plants, other animals feed on animals that feed on plants.
Plants use solar energy for immediate chemical reactions; they also use it to store energy in starch form. Without plants a lot of this energy would just disperse back into the atmosphere and back in space. Animals eat the plants, and in turn store energy. Of course, they also disperse some of the energy. But for an organism to survive, the total of the dispersed energy must always be less than the stored energy; even if energy is necessary to hunt and digest preys (the sources of energy). Natural selection must favor efficient storage.
Clearly, a planet where life depends heavily on sunlight must harbor more energy than a planet without life. The problem is that some (a lot? How much? Why?) of this energy is stored, and passes from one form of storage to another. The planet would only be hotter if life consistently releases more energy than is currently being absorbed from outside into stored form, that is, releasing energy that had been stored in the past and not used (for example, animals eating a stock of very old trees, or humans burning fossile fuels). Obviously, that kind of situation can only go on as long as the stock of “old” energy lasts, so it is only a temporary state. Therefore we should try to measure stored energy, not the energy being currently dispersed in heat form, which is what temperature measures.
Unfortunately, the only way to measure how much energy is stored somewhere without having access to the history of the object is to burn it down and see how much energy is released in heat form. Burning down entire planets is not a very convenient way to proceed. We are better off looking for indirect signs that energy might be stored somewhere, by detecting small pockets of variable heat isolated from sources of constant heat.
One of the best science books I read this year is “Superforcasters”, by Philip Tetlock. The story of how this book got to be written is just about as fascinating as the book itself, and I strongly recommend it to both scientists and non scientists.
Today I would like to talk about something that I am surprised wasn’t discussed in the book. As many posts on this blog, this is something that may or may not be an original idea: all I know is that it occurred to me and I thought it was worth sharing, and I haven’t heard of it in the forecasting world.
Early in the book, Tetlock gives an example of the “wisdom of the crowd”. At a fair, people are asked to guess the weight of a cow. Taken individually, some guesses are quite far from the real value. But the average of all the guesses turns out to be almost exactly equal to the real weight of the cow.
He uses that example to illustrate the fact that individual people can be biased, but when you average all the guesses, the biases cancel each other. Imagine each guess as having two components: the signal and the noise. The signal represents all the valid reasons why a person might have a good estimation of the weight of the cow: they know what is a cow and what things weight in general, and maybe this particular person grew up in a farm and knows really well about cows, or maybe they’re a weightlifter and knows really well about weights. The noise represents all the reasons why they might be biased. Maybe they’re a butcher and often overestimate the weight of what they sell to increase the price. Maybe they raise pigs and underestimated the weight of the cow because it’s so much bigger than a pig.
By averaging all the guesses, you are making strong assumptions.
You assume that people’s biases are opposite and equivalent.
Therefore by averaging, the noise components should cancel each other out and you should be able to get only the signal: the wisdom of the crowd.
These are reasonable assumptions that are used by default in many different fields. Noise is supposed to be random, while the signal contains information about something, therefore not is not random. Most people know what a cow is and most people know roughly what things weight. But in the case of human-driven forecasting, these assumptions are not perfect.
1. There is no reason why the bias should be evenly distributed. (In sciency terms: the probability distribution of the noise might not be a uniform distribution). If your crowd is made of 30 cheating butchers (overestimating weights) and 10 greedy clients (underestimating weights), your biases may be opposite but they are not evenly distributed. Even if the clients bias happen to be exactly opposite to the butchers bias, averaging the 40 guesses will not give you the right answer, because you have many more butchers in your population. It will give you an overestimated weight. Instead you should pool the data: average the clients guesses (pool A), average the butchers guesses (pool B), and then take the average of the results of of pool A and B.
2. There is no reason why the biases should be exactly opposite. (The distribution of the noise might not be 0-mean).
Ideally, you would know by how much butchers tend to overestimate (say on average +5% of the total weight) and by how much the clients tend to underestimate (say -10%). If you have this information, you can use it to weight your pooled data before putting them together. In this example, you would want to give less weight to the clients pool because you know that usually, their bias is higher than that of the butchers.
So if you have some forecasting data and you want to get the best forecast out of it, there are two things you should do before making averages.
First, identify all possible sources of biases and form pools based on this information. Repeat this step as many times as needed for different repartitions. If you are doing political forecasting, people might be biased in favor of their candidate: divide your data in political parties (repartition A). If women tend to have different political biases than men for some reason, identify that reason and divide your pool in men and women (repartition B). The more (verifiable) causes for bias you can find, the more you will be able to cancel them out.
Second, quantify the bias so you can attribute weights to your pools. For that you will have to rely on previous data and make guesses.
Finally, make your averages per repartitions. You will have as many averages as the number of repartitions you made. You can decide to make a final average out of this data, or you can go meta and give weights to your repartitions. If you are quite sure that repartition A captures a real cause for opposite biases, but less sure about B, give less weight to B.
Now of course, it should be noted that it isn’t always worth doing all this work. If you have data about guessing a cow’s weight, maybe just do a simple average. The result might be good enough and the extra work is not worth your time.
But if you are gathering data about whether country A and country B are going to start a war in the next 3 months, it might be worth putting a little bit more effort into pooling your data. It doesn’t have to be data directly produced by people: it can be governmental data, numbers from different agencies, it can be you trying to predict what people you know will do next… There is always place for bias anyway.
In addition, clearly identifying the source of bias in your data allows you to notice what data may be missing (if all your pools are biased in the same direction), and it allows you to update your forecasts efficiently. When you come into possession of new data, it can be hard to decide how much it should change your original forecast. But if you can readily identify to which pools the data belongs, updating is much easier.
Happy forecasting! The Good Judgement Open project is a good place to start (you don’t have to be a scientist at all, just give your opinion).
Bansky – Geisha from “Better in than out” – Wikimedia commons
I think all decisions we take are based on irrationality — but this irrationality can appear at different levels.
Paradoxically, when irrationality is at a deep level, opinions are easier to change. When irrationality is at the very last of the decision process, it is very difficult, if not impossible to operate change.
One of my most irrational opinions is that I love living in Japan. It is irrational in the sense that there is no reason for that opinion. I can make up reasons, I can rationalize my decision to live here: It’s a good place to do AI research, it’s full of good people, it has nice scenery.
But I knew none of that when I first visited here at 19 yo, and decided that I wanted to live here. This irrationality drove, from the top, my decision process; it is therefore difficult to convince me of changing my decision by giving me reasons why I should not love Japan.
Take someone who loves pasta. “I don’t think it tastes particularly good, and I know it’s a bit boring, but I just love pasta.”
You could tell them that spaghetti gives cancer and is made from dead skunks, they would have a hard time just starting to hate spaghetti.
Now take someone whose irrationality is much deeper in the decision process. “I love food that is made of wheat, and I heard my great grandpa was Italian, so I love spaghetti.” If you convince them that spaghetti isn’t made of wheat and that their great grandpa was Irish, they might just lose all interest for pasta.
You can change “love” by “hate”, “fear”, or any other emotion in the above examples. The point is that the level at which your emotions guide some of your decision processes determines how much you can be swayed by new facts.
And as much as I don’t understand America’s recent choice of president, I think that might be part of it. No amount of facts about that candidate could convince his followers that he wasn’t to be trusted. Maybe they are just in love with him. He says something and they interprete it as what they want to hear, and that is enough. They say he is actually a good person, a smart man, a competent businessman, that he respects woman and is not racist. Even when he himself says the contrary.
Of course, my decision to live in Japan is not supposed to destroy the life of millions of people. And maybe all of Trump voters actually made a rational choice, which is both extremely scary and leaves place to hope. But the way that election unfolded suggest that their choice is not based on facts, and therefore as irrational as can be.
Next year are the German and French elections, and a survey already revealed that the majority of French people would have chosen Trump if they could vote in the US elections.
What can be done? Unfortunately I do not have an answer.
For the past few years I have tried to deal with the worst of my irrational opinions, and the news are not good. Facts do not work. Pushing contradictory emotions does not work. Taking a step back has mixed results, but how do you force people to take a step back from politics? Replacing one irrational behaviour by another might work, from what I hear. I have not tested it. But if it is true, does it mean that the Trump crowd could only have been swayed by a candidate that they find more charismatic?
Given what their idea of charisma seems to be, I don’t know what a “more charismatic” candidate would have looked like.
Maybe we will discover it next year. Or maybe we will have to bow to President Le Pen.
Wolf pack surrounding a bison, via Wikimedia
Wikipedia cites altruism as “an evolutionary enigma”, because under current paradigms it is “evolutionary unstable”.
It means that when an altruistic individual appears in a group for the first time (by genetic mutation), its has a lower probability to pass its genes to the next generation, so altruism should always disappear shortly after appearing: altruism may benefit other members of the group but is detrimental for the altruistic individual itself. Even if altruism genes do spread in the whole group, if a single member evolves a selfishness gene, it will be advantaged by cheating on the other members and the gene for selfishness should take over the whole group.
Diverse models have been built to explain how altruism can have spread through a population, without disappearing from the start or from competition with selfishness. All are evolutionary unstable, so the puzzle is not solved.
Here is my model, and I do believe that it is evolutionary stable. Hopefully I will have time to code a simulation.
Hypothesis I: Vindictive behaviour is a precondition to the formation of societies.
Hypothesis II: A necessary condition for the apparition and continuation of altruistic behaviour is vindictive behaviour.
Hypothesis III: The individual cost of altruistic behaviour must always be balanced by the cost of retribution in case of non-altruistic behaviour.
These are three strong hypotheses… Let me explain what I mean by giving an example: food sharing in wolves. How could this real life behaviour have appeared?
Say you’re a lonely carnivore, ancestor of today’s wolves, but not living in groups. You hunt a prey and start eating, but then some creature comes and steals your food from you. Clearly, if your descendants evolve some genes that make them attack people who try or does steal their food, they will be better off than their naive conspecifics. It is even possible that the same genes that make you attack preys also make you attack other people, or other people’s preys… Maybe are you even one of the thieves that to steal other wolves’ preys in the first place? There is not much difference between a sick rabbit and a freshly killed rabbit, or between your dead rabbit and their dead rabbit… It is difficult to sort out the order in which these related behaviours (hunting, stealing, defending one’s food) appeared, and it is plausible that they all appeared conjointly.
Now say that for some reason, you find yourself stuck with several other pre-wolves on a small area. Maybe the population had a sudden increase in density. Maybe you’re all following the same herbivore migration. Anyway, now several of you have to eat their own prey at relatively short distance from each other. You’re not yet a society, but you do live together (think about today’s bears, who usually live alone or with their cubs but form big groups when it’s salmon season).
The first thing to happen might be that cubs stay closer to their mother, even as young adults, simply because there is not much space. Obviously mums share food with their cubs, but they also protect their cubs when they are eating. If, simply because they live close to each other, this behaviour persists once they are adult, the family will have an obvious evolutionary advantage by protecting each other’s food. They might even team up to steal solitary wolves’ food, or hunting bigger preys. On the other hand, those who don’t even bother to protect their own food don’t stand a chance in this new setting.
At this point, what prevents one member of the pack from cheating? You could eat more than your share, and stay away from battles to avoid danger. That would confer you a big advantage. This is what makes theories of altruism evolutionary unstable. Altruism should not be able to survive cheaters.
… Except if there is retribution. If you tend to take the biggest part of the prey and go away to eat it in peace, it might trigger the thief detector of your colleagues and they will attack you. If you don’t take part to the hunt, you may be considered as an outsider and attacked when you try to eat with the others. The apparition of such vindictive behaviour may not require much genetic change, but it has obvious advantages: it protects the group from cheaters, and it also represents a disadvantage for the cheater, who can be harmed, killed, or just starved as a result of its behaviour. In this group, cheating is the evolutionary unstable behaviour, while cooperation is stable.
But what about altruism? Imagine that instead of hunting all together, some wolves go hunting and then share with the whole pack (maybe because some members have to stay home to protect the cubs). In that case, they must obviously share with those who didn’t go hunting. Maintaining cheaters at bay means insuring that you don’t end up hunting alone while a whole group of lazy adult wolves wait for you to bring food, an easy way to game the system. Being vindictive or resentful is a defence mechanism that should bring the group to punish free riders before reaching that extreme situation.
Meanwhile, altruism should be partly motivated by the fear of social retribution, which is learned, and partly by genetic predispositions. I say that altruism should be learned, because cheating remains beneficial for a given individual, provided that the cheating is not big enough to be caught and punished and behaviours that are beneficial have not reason to disappear from the gene pool; but the punishment threshold depends on the current food resources and the character of other group members so it cannot be genetically encoded. Same goes for vindictive behaviour, which should be proportional to the offence to make evolutionary sense.
A consequence of this theory is that genes for the fear of social retribution should also be evolved, since it prevents the individual to get into too much trouble. At the same time, a race between better cheaters that don’t get caught and those who catch and punish them could also appear. Good cheaters will pass more genes on (and possibly also their tricks as knowledge), but they might also be better at catching members who use the same tricks as them, maintaining balance.
It is possible to game the system by not exhibiting vindictive behaviour. It is costly to monitor and punish cheaters, so you can try to count on others to do it for you and save your energy for more important things. Except of course if this kind of slacking is also punished (just think about all the people who get angry both at what they see as immoral behaviour and at those who refuse to be indignant at such behaviour). Who would have believed it! Vigilantism, self-righteousness, jealousy and charity, sharing, benevolence, all linked together… (I do not endorse vindictive behaviour, by the way.)
This walkthrough can, I think, be applied to most altruistic behaviours. Some howling monkeys give alarm calls when a predator approach the group, which make them more likely to be spotted and killed by said predator. This is a behaviour that is clearly very costly in terms of survival chances. The group can only resist to cheaters if there is a form of punishment that is even more costly (I don’t know if cheaters are punished in these groups of monkeys, but I expect so). The loss caused by altruistic behaviour must always be lower than the cost of retribution to maintain evolutionary stability.
Once it has appeared and found stability, altruistic behaviour can be enforced by other means than retribution, for example by ensuring that the individuals that have the possibility to cheat do not reproduce (like in social bees or mole rats). After all, it is also costly to the group to monitor and punish cheaters…
As you know, my passions in life are food and food. This blogpost is therefore about the taxonomy of window panes.
Sorry. This post is about FOOD! NYPL made a heap of information about New York food open access here; it’s the dataset I used to train my crazy twitter bot (@CrazyPoshCook), and you can find more examples of the bot’s output at the end of this post.
In their crowd-driven project, NYPL numerized data about more than 17 000 menus from NY restaurants between 1851 and 2012. There are regular menus, menus for special events, cruise menus… I delved into the data because I’m a serious scientist, not at all because I was hungry and bored. Here we go!
I first looked at which dish appeared more often in New York’s restaurants. To the surprise of no one, the most common menu item is… Coffee, with 8487 apparitions! In second position comes Tea (4769), then more surprisingly, Celery (4247), Olives (4554) and Radish (3349). NY people, you’re officially weird. The followers are somewhat more expected: mashed potatoes, milk, and boiled potatoes. Wait, who orders plain milk at a restaurant??
There are lots of items that appear only once, mostly dishes with really long names. Some dishes have a negative number of citations (that’s human error), like the awesome “Clam Fry (with Bacon)” from a 1914 menu (“-4” citations!).
The same kind of error popped up when I looked for the dish with the shortest name: it seems to be the mysteriously named “&”, which appeared on 4 different menus in 1901.
The dish with the longest “name” is a long ramble about tea that manages to include references to Elizabeth II and Lewis Caroll:
Afternoon Tea- A Great British Tradition- Tea, the most universally consumed of all drinks, is especially popular in Britain where the annual consumption is something in the region of 512 million cups. W. E. Gladstone observed “If you are cold, tea will warm you- if you are heated, it will cool you- if you are depressed, it will cheer you- if you are excited, it will calm you.” First brought to England c. 1559 by Giambattista Rusmusio, tea did not evolve into an afternoon meal until the end of the 18th century. Anna, Duchess of Bedford, invented afternoon tea to fill the long gap between early lunch and dinner which bored many house parties. It became a meal surrounded by etiquette and customs, delicate china, silver, cake stands and doilies- a time when friend and family meet. Famous tea parties include Mad Hatter’s (Alice’s Adventures in Wonderland by Lewis Carroll 1865), the Boston Tea Party, 1773, and not forgetting HM Queen Elizabeth II’s annual garden parties at Buckingham Palace. The Duke of Wellington declared that “Tea cleared my head and left no misapprehensions.” He was right- tea contains small amounts of two B vitamins, and has no calories, artificial flavourings or colourings. It is said to cure gout, apoplexy, epilepsy, gall stones and sleepiness, and one’s longevity is assured. “Thank God for Tea! What would the world do without tea?”- Sydney Smith
But that’s cheating – there’s nothing about the actual tea they serve you. So the real laureate is the famous Tour d’Argent of Paris, with this lengthy but delicious-sounding single dish from 1987:
Fresh Water Prawn Rampant, Baby White Fish, with Timbal of Transylvanian Macadamia Nuts, Sea Scallops, Two Gunkan Rolls of American Sturgeon and Salmon Caviars, served on Wasabi Sauce Rouille- The fresh water prawn is from an American based farm and is split and baked in a hot rouille sauce. One prawn is served along side the baked white fish. It is served under a timbal made with sea scallops and alongside two Chinese rice rolls filled with two caviars. Rouille is similar to a hot Hollandaise. The sauce is made with wasabi powder and cream.
Price unknown. Oh gods. While we’re on the subject, let’s have a look at the priciest items. Ordering by highest “highest_price” gave ludicrous results (a $2550 grape fruit… Is it from the Hesperides’ Garden?!?) so I ordered the data by highest “lowest_price” instead. The winner is some “Chicken Liver Omelette”, at $1035! Yes, I checked the currency. Here are the 10 priciest dishes:
Lots of champagne, and a… ham sandwich?
Next I liked at old dishes. The oldest entries are from 1851, but most of them appeared only once, so instead I looked for old dishes that lasted for more than a year. I thought they would be more representative of what food was common at the time:
We have some weird ones! My favorite is the stale bread. Next I wondered what were the dishes that had the longest lifespan:
Super boring, but those are some pretty expensive peaches 0_0
I had to Google “Charles Heidsieck”. It’s champagne. Oh, and mashed potatoes can cost you more if you ask it with a capital P.
The menus with the most gigantic number of dishes all come from “Waldof Astoria”, with more than 1000 dishes to choose from for a single occasion! Here is what a page looks like:
Wow.
So that’s some tidbits about the dataset I used. The bot was super fun to train, here are some screenshots that made me cry laughing (because I’m a bit crazy too I guess).
See you next time!
Hi tweeps (I know most of you arrive here via Twitter (except for that one US bot who watches the same 10 pages every night (hi you!)))
So I’m sitting in the Tokyo-Sidney plane, which has no power plugs and broken headphones, and I thought, what can I do while waiting to land on the continent with the weirdest fauna in the world?
The answer is, talk about my own computer generated weird species of course. This post is the follow up to this one and this one, and to a lesser extent, this and this. Actually the results have been sitting in my computer since last summer; I posted a bit on twitter too. In short, OEE is about building a living world that is “forever interesting”. Since you’ve got all the theory summed up in the previous posts, let’s go directly to the implementation and results.
To be honest, I don’t remember all the details exactly. But here we go!
Here is what the 1st batch looked like, at the very beginning of the simulation:
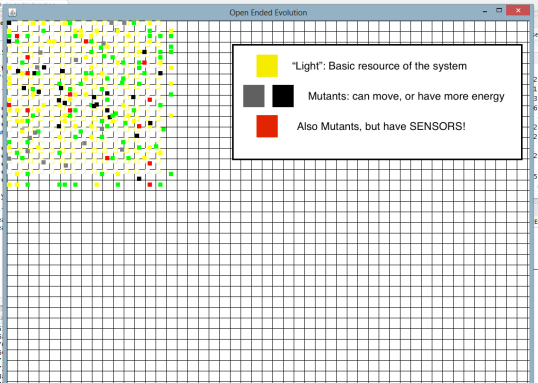
So you have an artificial world with individuals that we hope will evolve into something interesting through interactions with each other. The yellow individuals are how we input free energy in the system. It means that they appear every few steps, “out of nothing”. They cannot move, or eat, or do anything interesting really. They just contain energy, and when the energy is used up, they die. I call it “light”.
Then you have the mutants, which appear on the field like light, but with a random twist. Maybe they can move, or hypothetically store more energy. Mutants can produce one or more kids if they reach a given energy threshold (they do not need a mate to reproduce.) The kid can in turn be copy of their parents, or mutants of mutants.
Then you have the interesting mutants. These have sensors: if something has properties that their sensors can detect, they eat it (or try to). Eating is the only way to store more energy, which can then be used to move, or have kids, or just not die, so it’s pretty important.
Now remember that this sim is about the Interface Theory of Perception. In this case it means that each sensor can only detect a precise value of a precise property. For example, maybe I have a sensor that can only detect individuals who move at exactly 1 pixel/second. Or another sensor that detects individuals that can store a maximum of 4 units of energy. Or have 2 kids. Or have kids when they reach 3 units of energy. Or give birth to kids with a storage of 1 unit of energy.
A second important point is, you can only eat people who have less energy than you do, otherwise you lose energy or even die. BUT, to make things interesting, there is no sensor allowing you to measure how much energy this other guy has right now.
It sounds a bit like the real world, no? You can say that buffaloes that move slowly are maybe not very energetic, so as a lion, you should try to eat them. But there is no guarantee that you will actually be able to overpower them.
Before we get there, there is a gigantic hurdle. Going from “light” to lions or buffaloes is not easy. You need sensors, but sensors require energy. And mutations appear randomly, so it takes a lot of generations to get the first viable mutant: something that can detect and eat light, but doesn’t eat their own kids by mistake. Here is what the origin of life looks like in that world:
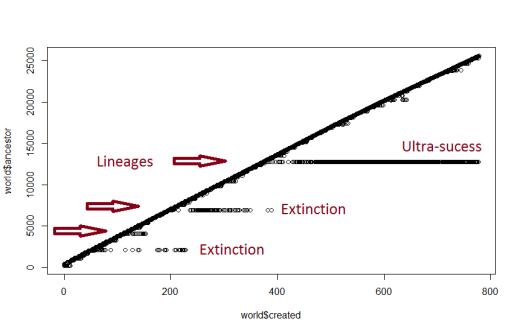
The Y axis is the ID of the oldest ancestor, and X is the time. Everything on the diagonal is just regular light. All the horizontal branches are mutant lineages; as you can see, there are lots of false starts before we get an actual species to get off! Then at a longer timescale this happens:
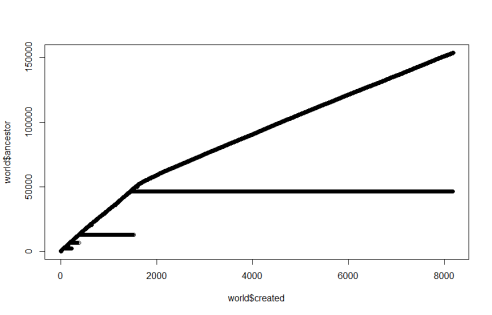
This is the same sim as before, but zoomed out. Lots of interesting stuff here. First, or previously successful descendants of #14000 go extinct just as a new successful lineage comes in. This is not a coincidence. I think either both species were trying to survive on the same energy source (light) and one starved out the other, or one just ate the other to extinction.
Seeing as the slope of the “light” suddenly decreases as species 2 starts striving, I think the 1st hypothesis is the right one.
Now the fact that our successful individuals all have the same ancestor doesn’t actually mean that they belong to the same species. Actually, this is what the tree of life looks like in my simulated worlds:
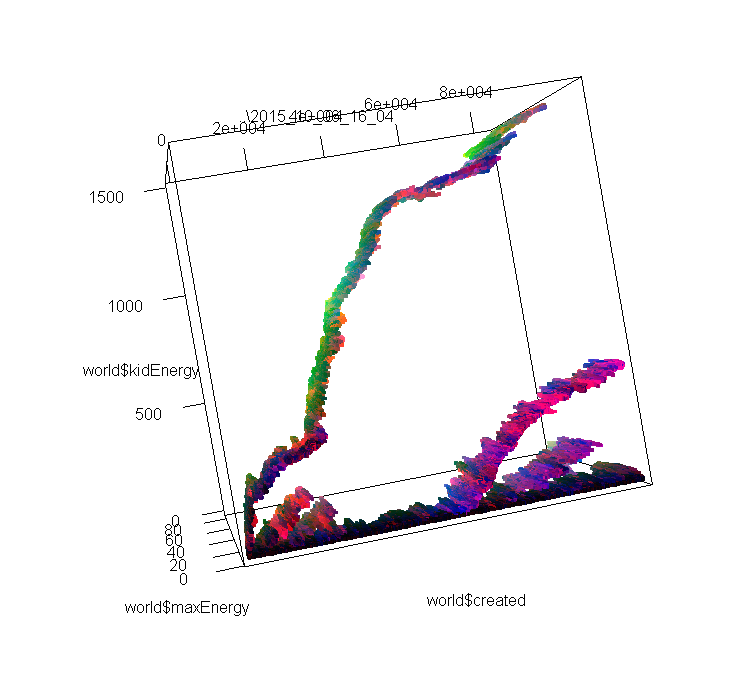
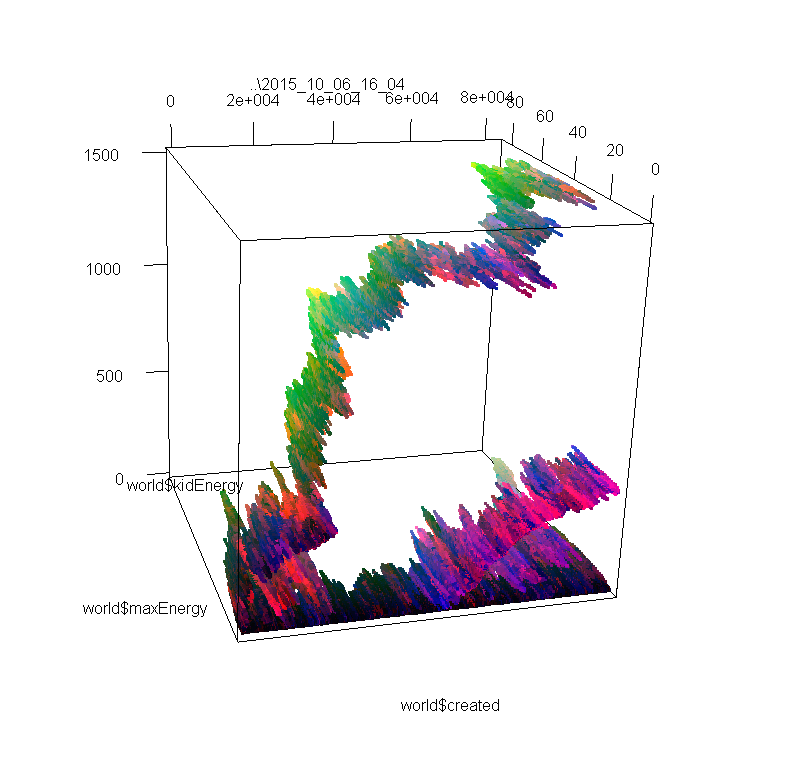
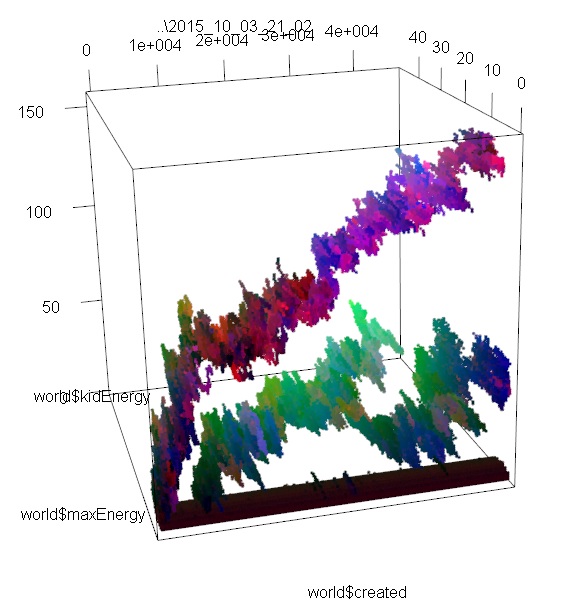
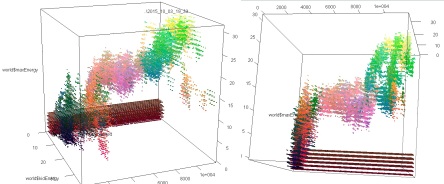
These images represent the distribution of individuals’ properties through time. I encoded 3 properties (don’t remember which) in RGB, so differences in colors also approximately represent different species, or variations in species. In images 1 and 2, you can see 2 or 3 different branches with different ancestors. On these I was only looking at the max amount of energy that each individual can store, and how much of this energy is passed from the parent to its kids. If I had looked instead at speed, or at the number of sensors, we may have seen the branches divide in even smaller branches.
In the 3rd image, we see much more interesting patterns; the lower branch divides clearly in 2 species that have the same original ancestor; then one branch dies out, and the other divides again, and again! To obtain these results, I just doubled the area of the simulation, and maybe cranked up the amount of free energy too (the original one was extremely extremely tiny compared to what is used in Artificial Life usually. Even when doubling the area, I don’t think I ever heard about such a small scale simulation.).
Still, the area was bigger but one important motor of speciation was missing. In real life, species tend to branch out because they become separated by physical obstacles like oceans, mountains, or just distance. To simulate that, I made “mobile areas” of light. Instead of having a fixed square, I had several small areas producing light, and these areas slowly move around. It’s like tiny islands that get separated and sometimes meet each other again, and it looks like this:
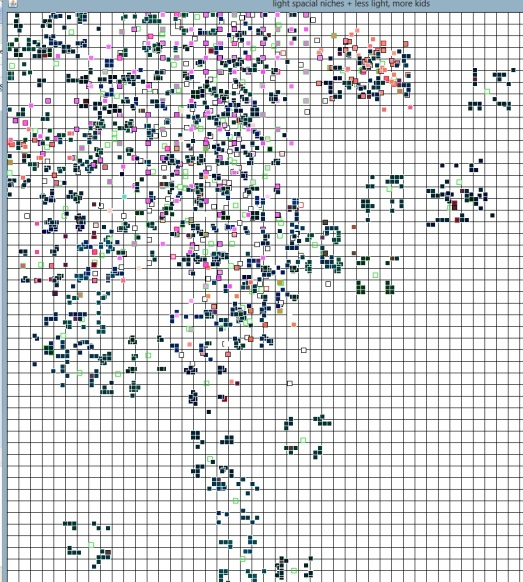
Now the species have to follow the light sources, but they can also meet each other and “infect” each other’s islands, competing for resources (or just to eat each other). The trees you get with this are like this:
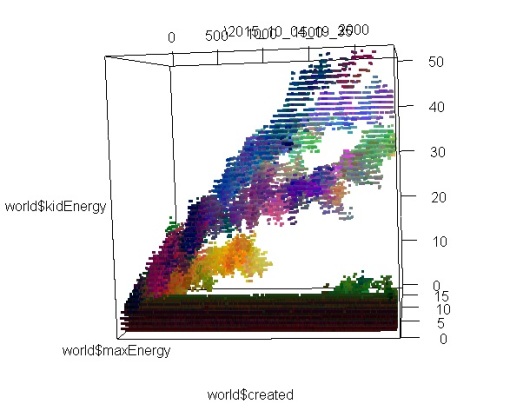
Even more interesting! So many branches! And just looking at the simulation is also loads of fun. Each one is a different story. Sometimes there is drama…
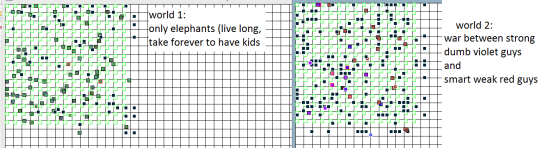
I was rooting for the “smart guys” (fast and with many sensors) above, but they eventually lost the war and went extinct.
What do we take out of that? First, some of the predictions I made in previous posts got realised. The Interface Theory of Perception does allow for a variety of different worlds with their own histories. Additionally, refusing to encode species in the simulation does lead to interesting interactions, and speciation becomes an emergent property of the world. Individuals do not have a property names “species”, or a “species ID” written somewhere. Despite that we don’t end up with a “blob of life” with individuals spread everywhere, we don’t have a “tree of life” clean and straight like in textbooks. It’s more of a beautiful mutant broccoli of life, with blobs and branches. And this sim doesn’t even have sexual reproduction in it! That would make the broccoli even cooler.
The next step in the sim was to implement energy arrays, as I mentioned in an earlier post. I already started and then I kinda forgot. Hopefully I’ll find time to do it!
Conclusion: Did I build an OEE world? Ok, probably not. But I like it and it lived to my expectations.
itakoyak 